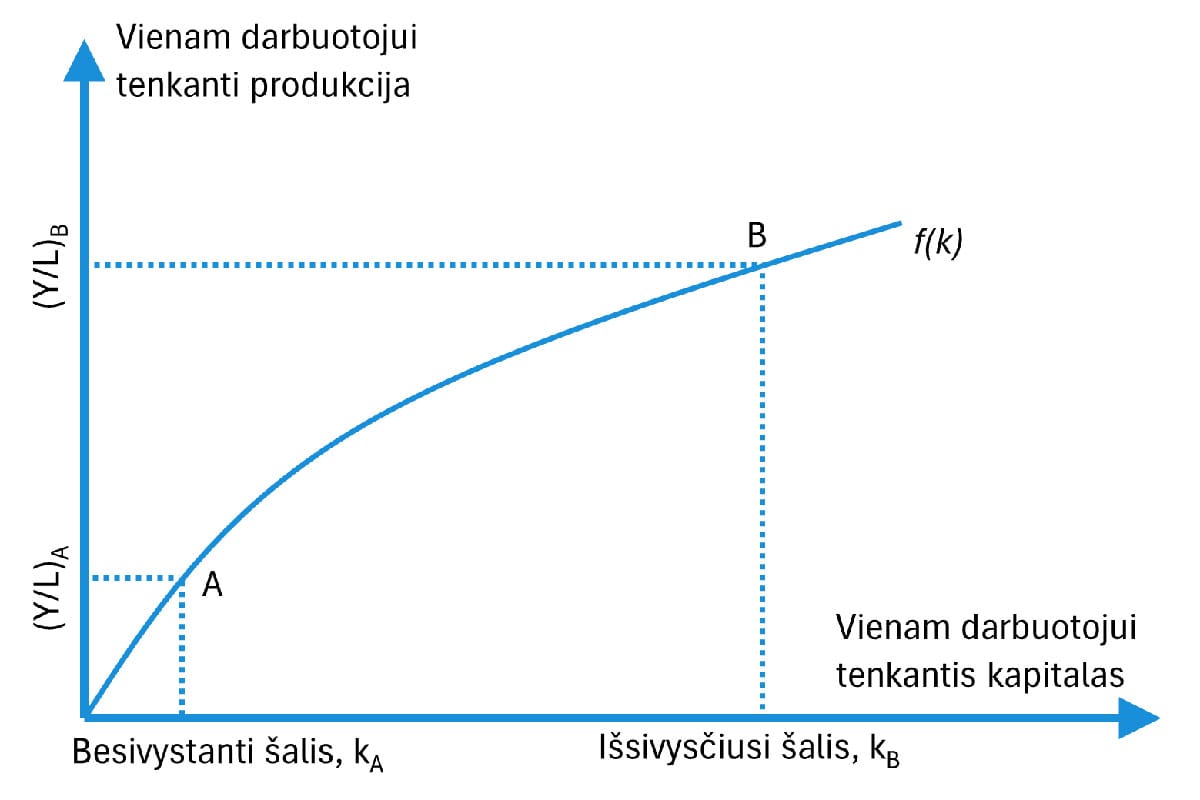
Subalansuotas arba stabilus augimo tempas

Kaip ir daugelyje ekonomikos modelių, neoklasikiniame augimo modelyje siekiama apibrėžti pusiausvyros padėtį, kurios link ekonomika ilgainiui juda. Solow modelio atveju ši pusiausvyra – tai subalansuotas (arba stabilios būsenos) augimo tempas, kuris nusistovi tada, kai gamybos ir kapitalo santykis išlieka pastovus. Toks augimas vadinamas subalansuotu, nes vienam darbuotojui tenkantis kapitalo kiekis ir vienam darbuotojui tenkanti gamyba auga tuo pačiu tempu.

Cobb-Douglaso funkcijos taikymas vienam darbuotojui

Analizę pradedame nuo anksčiau pateiktos Cobb-Douglaso gamybos funkcijos formos, pritaikytos vienam gyventojui:

y=Y/L=Ak^α

kur k=K/L. Atsižvelgiant į apibrėžtis, kapitalo ir darbo jėgos santykio bei vienam darbuotojui tenkančios produkcijos augimo tempai yra tokie:

Δk/k=ΔK/K−ΔL/L ir Δy/y​=ΔY/Y​−ΔL/L​

Kadangi y=Ak^α, iš gamybos funkcijos gauname:

Δy/y=ΔA/A+αΔk/k

Kapitalo kaupimas ir investicijos

Ekonomikoje fizinio kapitalo atsargos (K) didėja dėl investicijų (I) ir mažėja dėl nusidėvėjimo. Uždaroje ekonomikoje investicijos finansuojamos iš santaupų. Jei s yra santaupoms tenkanti pajamų (Y) dalis, tuomet I=sY. Tarkime, kad kapitalo nusidėvėjimo tempas yra pastovus δ. Tuomet kapitalo atsargų pokytis:

ΔK=sY−δK

Darbo jėgai didėjant sparta n, iš čia išvedame:

Δk/k=sY/K−δ−n

Stabilios būsenos augimo tempas

Esant stabiliai būsenai, kapitalo vienam darbuotojui augimo tempas sutampa su produkcijos vienam darbuotojui augimo tempu, taigi:

Δk/k=Δy/y=ΔA/A+αΔk/k

Iš to galima gauti:

Δy/y=Δk/k=(ΔA/A)/(1−α)

Tarkime, kad θ≡ΔA/A žymi TFP (bendrojo gamybos veiksnių produktyvumo) augimo spartą. Tuomet pusiausvyros tvarus vienam gyventojui tenkančios produkcijos augimo tempas (arba kapitalo vienam darbuotojui augimo tempas) priklauso tik nuo θ ir α:

(Gamybos vienam gyventojui augimas)=θ/1−α

Pridėję darbo jėgos augimo tempą n, gauname visos produkcijos tvarų augimo tempą:

(Bendras gamybos augimas)=(θ/1−α)+n

Tai – pagrindinis neoklasikinio modelio rezultatas. Pastebėkime, kad θ/1−α ​ rodo stabilų darbo našumo augimo tempą, atitinkantį aptartos „darbo našumo augimo apskaitos“ logiką.

Pastovus produkcijos ir kapitalo santykis

Įstačius θ/1−α lygtį ir pertvarkius, gaunamas pusiausvyros gamybos ir kapitalo santykis, žymimas Ψ. Stabilioje būsenoje ši reikšmė pastovi, todėl kapitalo ir darbo santykis k, taip pat vienam darbuotojui tenkanti produkcija y, didėja minėtu tempu θ/1−α​. Tuo pačiu kapitalo ribinis produktas išlieka nekintamas ir, pagal Cobb-Douglaso gamybos funkciją, lygus α(Y/K). Net jei k laikui bėgant toliau auga, tai nekeičia ribinio kapitalo produktyvumo: pasiekus stabilią būseną, papildomas kapitalo gilinimas nebepaveikia ekonomikos augimo tempo ar kapitalo ribinio produkto.

Intuityvi interpretacija: taupymo ir investicijų pusiausvyra

Galima ir intuityviau paaiškinti lygties stabilią pusiausvyrą, ją išreiškiant santaupų–investicijų lygtimi:

s y=[(θ/1−α)+δ+n]k

Subalansuotas augimas nusistovi ties tokiu produkcijos ir kapitalo santykiu, kad ekonomikoje sukuriamų santaupų (sy) visiškai pakanka:

1. aprūpinti kapitalu naujus darbuotojus, kurių skaičius didėja sparta n,
2. kompensuoti kapitalo nusidėvėjimą, kuris vyksta sparta δ,
3. didinti fizinio kapitalo atsargas θ/1−α sparta, kurios reikia, kad kapitalo ribinis produktas būtų lygus jo nuomos kainai.

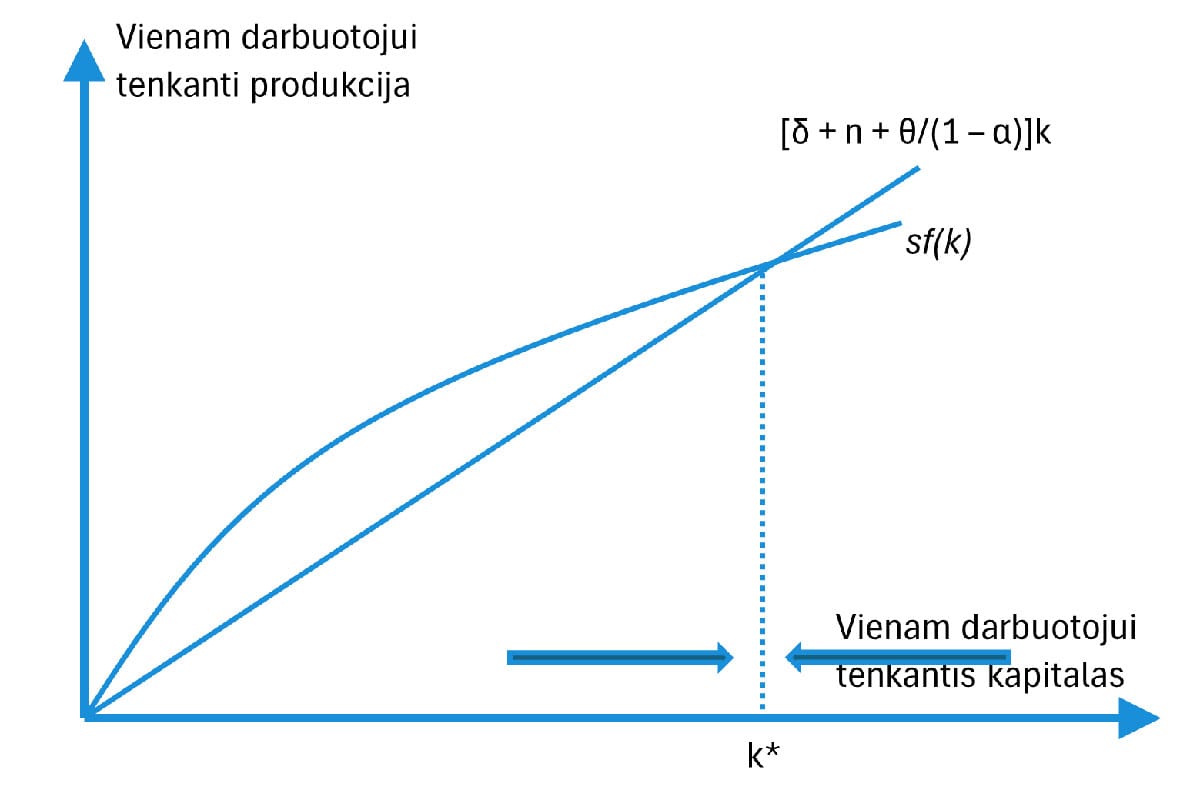
Grafiškas stabilių investicijų ir taupymo vaizdas

1 pav. rodo šią pusiausvyrą grafinėje erdvėje. Tiesė, kurios nuolydis δ+n+(θ/1−α)​, žymi reikiamą investicijų kiekį, palaikant kapitalo augimą reikiamu tempu. Lenkta kreivė sf(k) aprašo faktinį santaupų ir investicijų dydį vienam darbuotojui (tai taupymo norma padauginta iš gamybos funkcijos). Ji yra išlenkta dėl mažėjančio ribinio kapitalo produktyvumo. Susikirtimo taškas parodo stabilią pusiausvyrą. Laikui bėgant, augant TFP, kreivė [sf(k)] slenka aukštyn, tad kapitalo kiekis vienam darbuotojui didėja reikiamu tempu, o pusiausvyra juda dešinėn bei aukštyn.

1 pav. Neoklasikinio modelio pastovioji būsena

Modelio parametrų poveikis stabiliai būsenai

Kadangi stabilaus augimo kelyje ∗ laiko momentu laikome darbą ir TFP pastoviais, galime klausti, kaip įvairūs parametrai veikia ilgalaikę pusiausvyros padėtį (t. y. k ir y):

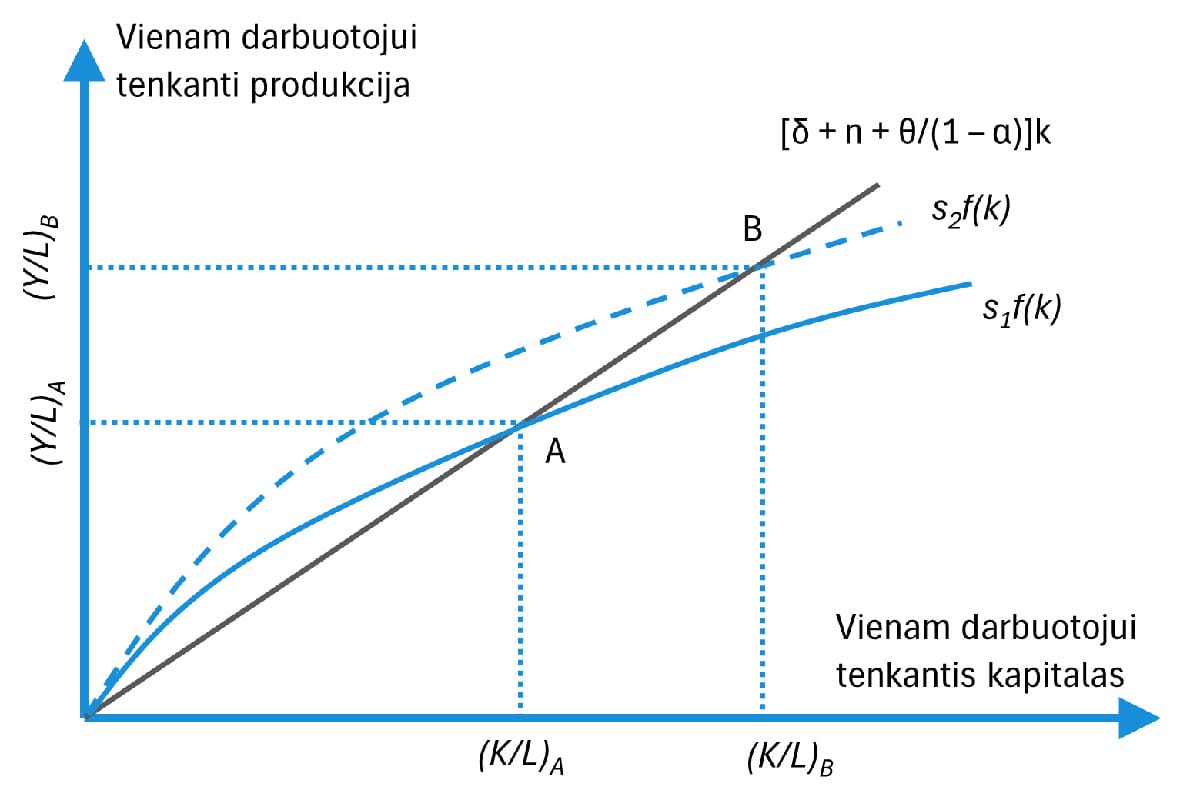
1. Taupymo norma (s): Didesnė s reiškia didesnį kapitalo ir darbo santykį k ir didesnę produkciją vienam darbuotojui y. 2 pav. parodo, kaip [s₁f(k)] pakilimas į [s₂f(k)] lemia naują stabilią pusiausvyrą su aukštesniu k ir y. Tačiau tai nepakeičia stabilaus augimo tempo θ/1−α ​.

2 pav. Poveikis stabiliai būsenai: Taupymo normos padidėjimas

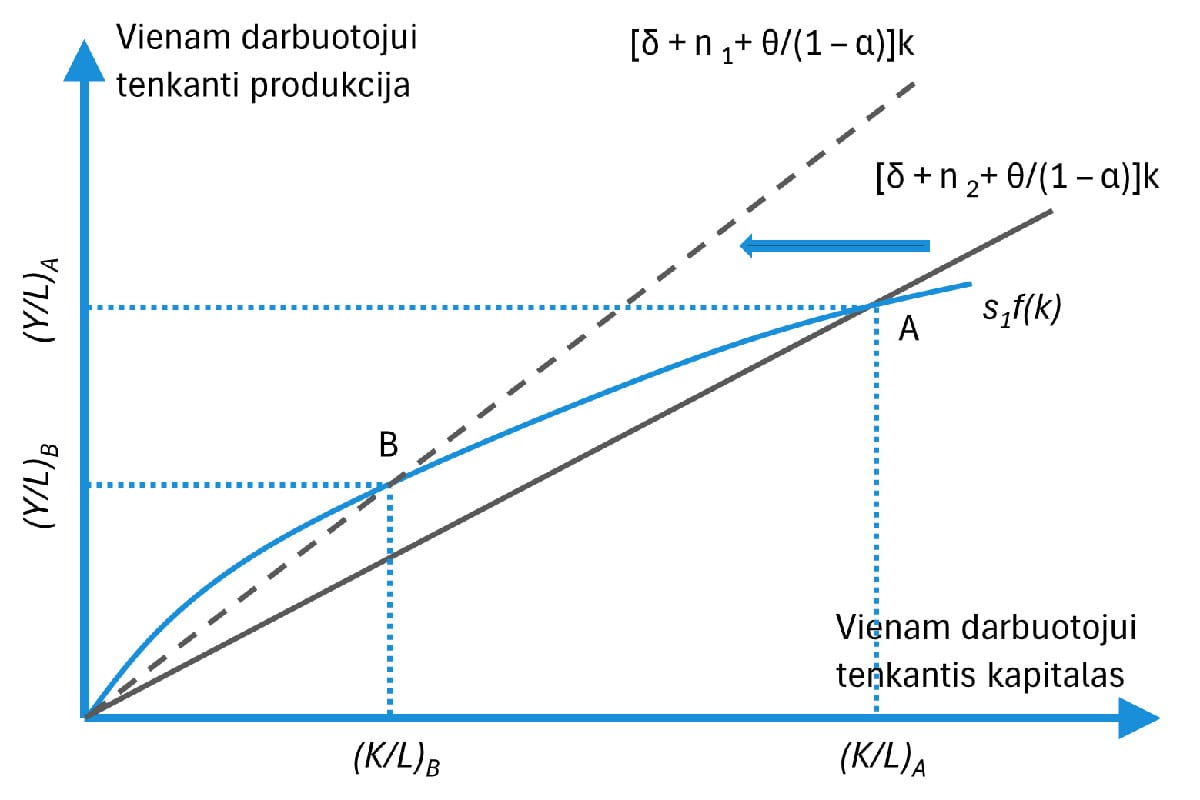
2. Darbo jėgos augimo tempas (n): Padidėjus n, reikia didesnio kapitalo augimo vienam darbuotojui, todėl nusistovėjusios būsenos kapitalo santykis k mažėja. 3 pav. rodo, kad pakilusi reikiamų investicijų tiesė kerta taupymo kreivę žemiau buvusio k. Tokiu atveju mažėja ir y.

3. Nusidėvėjimo norma (δ): Veikia lygiai taip pat, kaip ir n: didėjantis δ reiškia, kad ekonomika praranda daugiau kapitalo kasmet, todėl pusiausvyros k (ir y) yra mažesni.

4. TFP augimo tempas (θ): Didesnė θ užtikrina, kad ateityje gamyba vienam darbuotojui augs sparčiau, tačiau tuo pačiu metu dabartinis pusiausvyros k (ir y) lygis krenta, nes reikia daugiau išteklių tam „pradiniam atotrūkiui“ padengti. Grafiškai tai reiškia statesnę reikiamų investicijų tiesę ir susikirtimo tašką, esant mažesniam k ir y.

3 pav. Poveikis stabiliai būsenai: Darbo jėgos augimo padidėjimas

Taigi šie veiksniai lemia vienkartinį pajamų lygio pokytį vienam darbuotojui, bet nepakeičia ilgalaikio produktyvumo augimo greičio. Norint padidinti nuolatinį produkcijos augimą vienam darbuotojui, reikia spartesnio TFP didėjimo.

Perėjimas į stabilią būseną

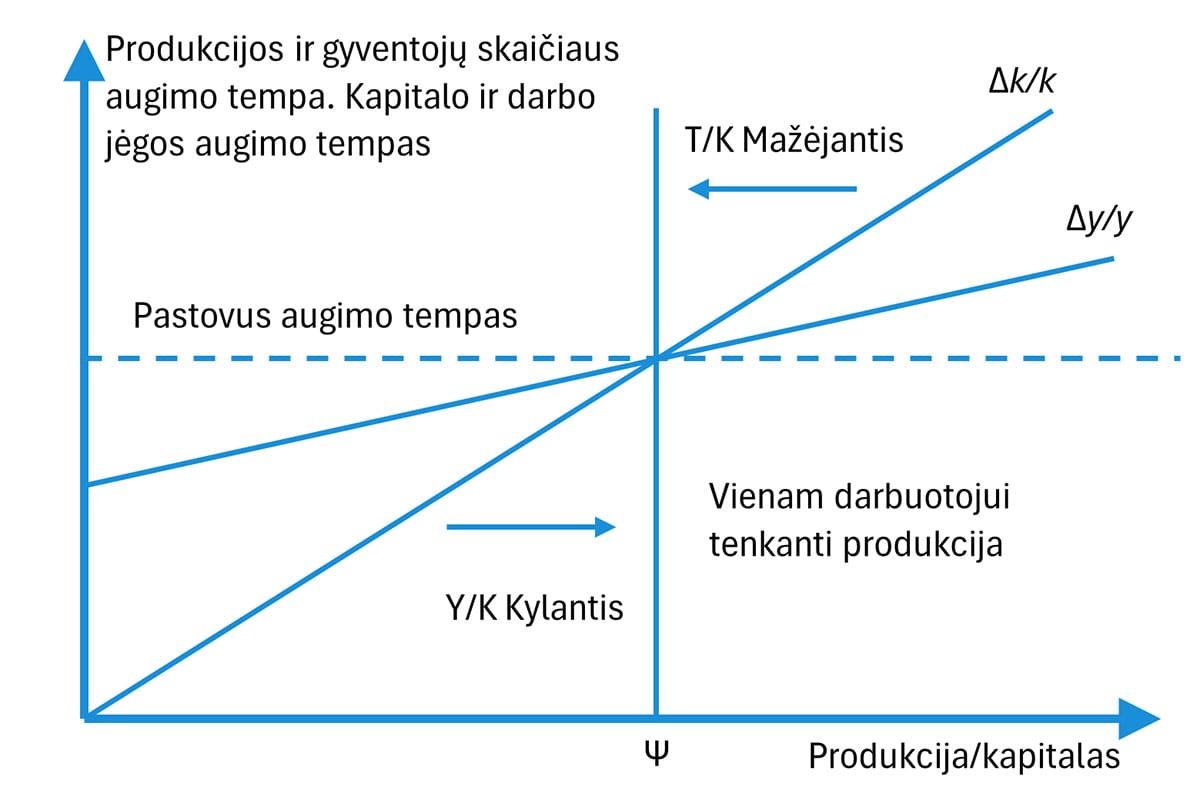
Iki šiol svarstėme tik stabilią būseną, bet kas nutinka, jei ekonomika dar jos nepasiekė? Pereinamuoju laikotarpiu augimas gali būti didesnis ar mažesnis už pusiausvyros tempą. Formulės rodo, kad:

• Jei faktinis Y/K​ santykis (gamyba ir kapitalas) aukštesnis už pusiausvyros Ψ, tuomet Δy/y ir Δk/k laikinai viršija θ/1−α ​. Tai dažnai reiškia, jog pradinėje padėtyje buvo mažas kapitalo ir darbo santykis, todėl investicijos greitai kelia bendrą produktyvumą.
• Priešingai, jei Y/K žemesnis už Ψ, investicijos nepakankamos, kad išlaikytų pusiausvyros tempą, ir augimas kurį laiką lieka lėtesnis. Tai paprastai reiškia, kad kapitalo ištekliai pradiniu laikotarpiu buvo pernelyg dideli lyginant su produkcijos lygiu.

Laikui bėgant, Y/K santykis priartėja prie Ψ, o augimo tempai linksta į stabilų θ/1−α​.

4 pav. Neoklasikinio modelio dinamika

Apibendrinimas

Neoklasikinis modelis parodo, kad ilgalaikio vienam darbuotojui tenkančios gamybos augimo negali nulemti vien tik didesnė taupymo norma, mažesnė nusidėvėjimo sparta ar lėtesnis darbo jėgos augimas. Šie veiksniai keičia lygio rodiklį (t. y. kiek prekių ir paslaugų tenka vienam darbuotojui), tačiau netvaraus augimo nesukuria. Vienintelis kelias į nuolatinį, ilgalaikį augimo greitėjimą yra TFP didėjimo (technologinės pažangos) spartinimas, nes tik tai pakelia visos ekonomikos produktyvumą stabilioje būsenoje.